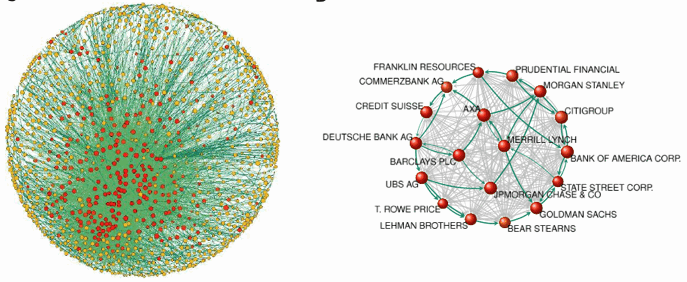
The Network of Global Corporate Control

Zu diesem Text siehe einführender Link: http://kommunisten.ch/index.php?article_id=1063 («ETH: Weltwirtschaft wir von 147 Firmen beherrscht»). Die Kommunistische Jugend hat anhand eines frei erfundenen Beispiels versucht, die Recherchen der ETH für alle zugänglich zu machen.

Einleitung

Eine Forschungsgruppe[1] der ETH Zürich untersuchte nach eigenen Angaben erstmals die globalen Kontrollmechanismen von transnationalen Konzernen. Motivation der Studie war, dass die Vernetzung transnationaler Unternehmen den globalen Wettbewerb beeinflusst und die Stabilität des Finanzsektors gefährdet, also für Politik und Wirtschaft von Interesse ist.

Dies führte zur Einsicht, dass einige wenige, stark untereinander verwobene, transnationale Unternehmen im Finanzsektor grössten Einfluss ausüben.

Methoden der Studie

Intuitiv (=Vermutung) sei die Dominanz weniger Unternehmen schnell ersichtlich, es sei jedoch schwierig, die Dominanz quantitativ (=zahlenmässig) zu erfassen, da Unternehmen über Besitzverhältnisse an anderen Unternehmen indirekt Einfluss nehmen können. Das Autorenteam hob hervor, dass gegenwärtige Wirtschaftstheorien nicht die Vernetzung von Unternehmen untereinander vorhersagen.

Daraufhin entwickelte das Autorenteam einige mathematische Methoden, um die Vernetzung quantitativ zu erfassen. Hier wird nur kurz auf die Grundidee eingegangen und erhebt keinen Anspruch auf Vollständigkeit.

Besitz bedeutet, eine Person oder Firma besitzt eine andere ganz oder teilweise. Die folgenden zwei Abbildungen zeigen den gleichen Graphen, einmal mit formalen Werten, einmal mit konkreten. Jeder Pfeil mit zugehörigem Wert gibt an, wie viel die Firma, von der der Pfeil wegführt, die andere Firma besitzt. Das Beispiel wurde willkürlich gewählt.

Solche Graphen nennt man „gewichtet“, da jeder Pfeil mit einem Wert versehen ist, der in diesem Fall in Prozent (100% = 1) den Besitzanteil an der anderen Firma angibt.

Links sind die Werte formal, rechts konkret angegeben.

Die Besitzverhältnisse fassen wir in einer Matrix W zusammen (eine sog. quadratischen Bewertungsmatrix), wobei der Eintrag w_ij angibt, wie viel die Firma i an j besitzt.

W_ij: i gibt die Zeile, j die Spalte an.

Matrix W	KJ	PdA Bern	PdA Zürich
KJ	W11 = 0.1	W12 = 0.3	W13 = 0.6
PdA Bern	W21 = 0.3	W22 = 0.4	W23 = 0.3
PdA Zürich	W31 = 0.6	W32 = 0.3	W33 = 0.1

Angenommen, die KJ, die PdA Bern und die PdA Zürich seien Aktiengesellschaften und bildeten die Weltwirtschaft:

Alle beteiligten Unternehmen sind durchnummeriert: KJ = 1, PdA Bern = 2, PdA Zürich = 3

Nun können wir aus der Matrix ablesen, wieviel der PdA Bern der KJ gehört:

KJ = 1, PdA Bern = 2

w₁₂ = 0.3

Die KJ besitzt 30% der PdA Bern

Die Matrix und der Graph sind jeweils eine andere Darstellungsform, beschreiben jedoch das gleiche System von Besitzverhältnissen. Die Matrixschreibweise wird gebraucht, damit der Computer mit den Daten rechnen kann.

Betrachtet man Abbildung 1 und 2, so fällt folgendes auf: Jeder Knoten (Firma) ist mit jedem anderen Knoten über zwei Wege verbunden. Einmal direkt und einmal über einen Zwischenknoten. Ein Pfeil zeigt von der KJ direkt zur PdA Bern, indirekt zeigt jedoch auch ein Pfeil über die PdA Zürich zur PdA Bern.

Die Studie berechnet nun neben dem direkten Besitzanteil, der mit den Pfeilen oder der Matrix direkt angegeben ist, auch einen indirekten Besitzanteil.

Im einfachsten Fall sieht dies laut Studie folgendermassen aus:

Besitz i j mit w_ij und j l mit w_jl, dann besitzt im einfachsten Fall die Firma i die Firma l mit w_ij*w_jl.

D.h. Folgt man den Pfeilen von der KJ zur PdA Zürich über die PdA Bern, so multipliziert man die Werte über den Pfeilen.

In unserem Beispiel besitzt die KJ die PdA Bern zu 30% und die PdA Bern die PdA Zürich zu 30%. Somit ist w₁₂ = 0.3 und w₂₃ = 0.3. Wir rechnen w₁₂*w₂₃ = 0.09 = 9%. Die KJ besitzt also indirekt 9% an der PdA Zürich zusätzlich zu den 60% die sie direkt besitzt.

In einem weiteren Schritt führt die Studie einen Wert zur Beurteilung des ökonomischen Wertes ein.

Sei nun v der ökonomische Wert einer Firma. v sei eine Liste mit den Einträgen v₁, v₂ usw. So beschreibt w_ij*v_j den ökonomischen Wert der Firma j, die die Frima i Besitzt.

Wir erweitern unser Beispiel mit der Liste der ökonomischen Werte, wieder völlig willkürlich

KJ	V1 = 0.2
PdA Bern	V2 = 0.3
PdA Zürich	V3 = 0.

Die PdA Bern hat nun einen Wert von 0.3. Die KJ besitzt 30% der PdA Bern. Rechnen wir nun w_ij*v_j so rechnen wir „Die KJ Besitzt 30% einer Firma mit dem Wert 0.3.“ 0.3*0.3 = 0.09

D.h. Die KJ besitzt durch die PdA Bern einen Wert von 0.09.

Bekanntlich besitzt die KJ indirekt 9% der PdA Zürich. Der ökonomische Wert, den die KJ somit indirekt besitzt, ist w12*w23*v₃ = 0.3*0.3*0.5 = 0.045. D.h. 9% vom Wert der PdA Zürich.

Die Studie entwickelt ihr Modell nun weiter.

Jeder Aktionär hat das Anrecht (juristisch), auf einen Teil des Firmengewinnes als Dividende und das Recht, Entscheidungen der Firma mitzubestimmen. Je grösser w_ij ist, desto mehr Kontrolle hat i über j da i nun mehr Aktien an j hat). Übersteigt w_ij den Wert von 50%, so ist i der Mehrheitsaktionär von j und unter voller Kontrolle. Die Matrix W wird nun nach dieser Regel zu einer Matrix C umgerechnet, wobei eine einfache Schwellenwertregel gilt: Der Mehrheitsaktionär besitzt volle Kontrolle und alle anderen keine. (Die Studie überprüfte auch Modelle, in denen die Minderheitsaktionäre einen Teil ihrer Macht behielten.) Schwellenwertregel heisst: Falls ein gewisser Wert (hier 50%) überschritten wird, so kommt die Regel zum Tragen, sonst passiert nichts.

Die PdA Bern wird zum Teil von der KJ als auch der PdA Zürich besessen. Es gibt jedoch keine Aktionärin mit mehr als 50%. Es passiert nichts. Bei der PdA Zürich sieht es anders aus. Sie wird mit 60% von der KJ besessen. Die KJ ist somit Mehrheitsaktionärin und besitzt faktisch 100%.

Aus dem neuen Graphen kann nun eine neue Matrix C gebildet werden.

Matrix C	KJ	PdA Bern	PdA Zürich
KJ	C11 = 0.1 → 0	C12 = 0.3 → 0.3	C13 = 0.6 → 1
PdA Bern	C21 = 0.3 → 0	C22 = 0.4 → 0.4	C23 = 0.3 → 0
PdA Zürich	C31 = 0.6 → 1	C32 = 0.3 → 0.3	C33 = 0.1 → 0

Nun beginnt die Studie damit konkret, Werte für die totale Kontrolle einer Firma zu berechnen.

Die Kontrolle über das gesamte Netz wird wie folgt berechnet: c_i^net = Σ_j C_ij*v_j + Σ_j C_ij*c_j^net. Dies entspricht der Kontrolle des Unternehmens i über alle anderen durch direkten Besitz von Aktien plus der indirekten Einflussnahme über alle anderen Unternehmen.

c_i^net ist eine Liste die angibt, wie viel Kontrolle das Unternehmen i insgesamt über alle anderen hat, d.h. wie viel das Unternehmen an allen anderen besitzt.

Σ_j C_ij*v_j ist die Summe aller direkten Besitztümer mal deren ökonomischen Wert.

Σ_j C_ij*c_j^net ist die Summe aller indirekten Besitztümer mal deren ökonomischen Wert.

Berechnen wir nun c₁^net, d.h. die gesamte Kontrolle der KJ. (Da Geld in einer Aktiengesellschaft gleich Macht ist, wird nun nicht mehr von Besitz sondern von Kontrolle gesprochen.)

Σ_j C_ij*v_j oder direkte Kontrolle:

Die KJ kontrolliert 30% der PdA Bern und 100% der PdA Zürich, sie kontrolliert also 30% des Wertes (also der Macht) der PdA plus 100% der Macht / des Wertes der PdA Zürich. Zusätzlich kontrolliert die KJ noch sich selber, jedoch nur zu 0% (PdA Zürich ist Mehrheitsaktionär), dieser Anteil fällt also weg.

Σ_j C_1j*v_j = 0.3*0.3 + 1*0.5 = 0.09 + 0.5 = 0.59

Doch damit noch nicht genug. Da die KJ die PdA Zürich kontrolliert, und diese wiederum die PdA Bern, kontrolliert die KJ also die PdA Bern zusätzlich noch indirekt.

Σ_j C_ij*c_j^net oder indirekte Kontrolle:

Da die KJ 30% der PdA Bern besitzt, besitzt sie auch 30% ihres Einflusses. Da die PdA Bern jedoch gar keinen Einfluss hat (sie wird in jeder Aktionärsversammlung von einer Mehrheitsaktionärin überstimmt), kommt hier genau 0 Einfluss dazu.

Bei der PdA Zürich sieht dies anders aus. Diese besitzt 30% der PdA Bern und 100% der KJ.

0.3*0.3 + 1*0.2 = 0.09 + 0.2 = 0.29

Zählen wir nun alles zusammen (0.59 + 0.29 = 0.88 = 88%), so erhalten wir, dass die KJ 88% der Wirtschaft kontrolliert.

Für die PdA Bern erhalten wir 0.12, also 12%, und für die PdA Zürich ebenfalls 88%.

Wir haben nun, ohne es zu wissen, rekursiv gerechnet. Um die Kontrolle der KJ zu berechnen, haben wir die Kontrolle der PdA Zürich berechnet. Unsere Rechnung brauchte das Ergebnis einer anderen Rechnung (des Einfluss der PdA Zürich).

Die Studie betrachtet ein viel grösseres Netzwerk, bei dem indirekte Einflussnahmen über viele Zwischenstationen möglich sind. Um dies zu berechnen, werden Verfahren zur schnelleren Berechnung eingesetzt. Auf diese wird hier nicht eingegangen.

Ergebnisse der Beispielrechnung

Die KJ kontrolliert 88% des Netzes, obwohl sie sich nur zu 10% selbst besitzt und dabei vom Mehrheitsaktionär PdA Zürich in jedem Fall überstimmt wird. Dies ist jedoch egal, da sie die PdA Zürich vollständig kontrolliert, also indirekt auch sich selber vollständig.

Die PdA Bern besitzt nur sich selbst zu einem gewissen Teil.

Die PdA Zürich besitzt ebenfalls 88% des Netzes. Zusammen gäbe das eine Kontrolle von 188% der drei Firmen über das gesamte Netzwerk. Dies ist jedoch natürlich nicht so. Da die KJ und die PdA Zürich sich gegenseitig vollständig besitzen, können sie als eine Einheit aufgefasst werden.

Ergebnisse der Studie

Durch das Aufsummieren vieler indirekter Einflussnahmen können einige Aktionäre sehr mächtig werden. In Graphen mit vielen Zyklen (Unternehmen besitzen sich gegenseitig) führt diese Berechnung zu überhöhten Kontrollwerten von einigen Firmen die sich in Zyklen befinden. In den Anhängen der Studie wird auf Methoden eingegangen, die dies zum Teil beheben.

Zur Berechnung wurden 43’060 transnationale Unternehmen nach dem OECD[2]-Standard aus über 30 Millionen ausgewählt. Durch rekursive Suche wurden die Besitzverhältnisse innerhalb dieser Unternehmen untersucht.

Die Studie beschrieb dabei eine Gruppe von Unternehmen, die als SCC (strongly connected component) bezeichnet wurden. In dieser Gruppe besitzt jedes Unternehmen Teile jedes anderen. Diese Strukturen wurden nur in kleinen Gruppen beobachtet und werden erklärt durch Anti-Übernahme-Strategien, Transaktionskostensenkungen, Risikoaufteilung und Interessengruppen. Dies wirkt dem Wettbewerb entgegen.

Beobachtet wurde auch, dass mächtige Unternehmen meistens zum sogenannten SCC gehören. Dabei kontrollieren 147 um die 40% des gesamten Netzes und haben damit beinahe vollständige Kontrolle über sich selber. Ca. 75% dieser Unternehmen gehören der Finanzbranche an.

Übereinstimmende Beobachtungen der Studie und der Beispielrechnung

Die KJ und PdA Zürich gehören der Studie nach zum SCC und passen relativ gut in diese Definition.

Die KJ erhält ihre Macht indirekt durch aufsummieren indirekter Werte.

„In Graphen mit vielen Zyklen (Unternehmen besitzen sich gegenseitig) führt diese Berechnung zu überhöhten Kontrollwerten von einigen Firmen, die sich in Zyklen befinden.“ Das trifft auf die KJ und PdA Zürich zu, sie kontrollieren 176% von allem (also ein ziemlich überhöhter Wert.)

Alle Mächtigen Unternehmen gehören zum SCC.

Anmerkung zu Mathematischen Modellen

Die Studie entwickelte ein mathematisches Modell, um in der Wirklichkeit herumzurechnen. Um ein Modell zu erhalten, wurden einige einfache Annahmen getroffen (z.B. Besitz i j mit w_ij und j l mit w_jl, dann besitzt im einfachsten Fall die Firma i die Firma l mit w_ij*w_jl.) oder dass der ökonomische Wert mit Einfluss gleichgesetzt wird.

Auch wenn alles richtig berechnet worden ist und alle Informationen über die untersuchten Firmen stimmen, kann trotzdem alles falsch sein, wenn die Grundannahmen falsch sind.

Zu diesem Thema gibt es drei Texte (der gleiche Text unterschiedlich ausführlich und unterschiedlich mathematisch) von Prof. Dr. Claus Peter Ortlieb Fachbereich Mathematik der Universität Hamburg.

http://www.math.uni-hamburg.de/home/ortlieb/

Texte:

ñ    Mathematisierte Scharlatanerie. Zur ‹ideologiefreien Methodik› der neoklassischen
Lehre

ñ    Markt-Märchen…

ñ    Methodische Probleme und methodische Fehler der mathematischen Modellierung in der
Volkswirtschaftslehre

In diesen Texten wirft Ortlieb der Volkswirtschaftslehre grobe Fehler in der Modellbildung vor.

Auch die soeben behandelte ETH-Studie wurde diesbezüglich nicht kritiklos wahrgenommen.

Rückfragen: info@kommunistischejugend.ch

---

[1] Stefania Vitali, James B. Glattfelder, Stefano Battiston

[2] Organisation für wirtschaftliche Zusammenarbeit und Entwicklung – Organisation for Economic Co-operation and Development